Vào đầu năm 1944, quân Đức bắt đầu đánh bom rải thảm miền nam nước Anh, nhằm tiêu hao sinh lực quân đội Đồng minh. London là một trong những nơi chịu tác động vô cùng nặng nề. Với bom bay V-1 (tiền thân của tên lửa hành trình), quân Đức có thể phóng V-1 từ bờ biển Pháp và Hà Lan vào lãnh thổ Anh. Theo thống kê, từ tháng 6 đến tháng 10 năm 1944, Đức đã phóng 9521 quả V-1, trong đó 2419 quả đã đến mục tiêu ở London.
Lúc này, vấn đề hệ trọng của quân đội Đồng minh là xác định xem, liệu có phải quân Đức có vũ khí hay thông tin mật hay không, vì lượng bom khá tập trung ở một số điểm. Nếu đúng là quân Đức phóng có mục tiêu cụ thể chính xác, thì chắc chắn quân Đồng minh gặp rắc rối lớn: thông tin đã bị rò rỉ.
Nhiệm vụ hệ trọng này được giao cho các nhà toán học. Nhà thống kê học R. D. Clarke sau này đã trình bày trong một bài báo năm 1946, sau khi quân Đức đã đầu hàng. Đầu tiên, ông lấy một khu vực rộng 12×12 km, và chia nhỏ thành 576 ô vuông bằng nhau. Khu vực này có 537 quả bom rơi trúng. Từ đó, Clarke đếm được ở mỗi ô có bao nhiêu quả bom rơi, và có được bản đồ sau (mình đã tô màu để bạn nhìn rõ hơn):
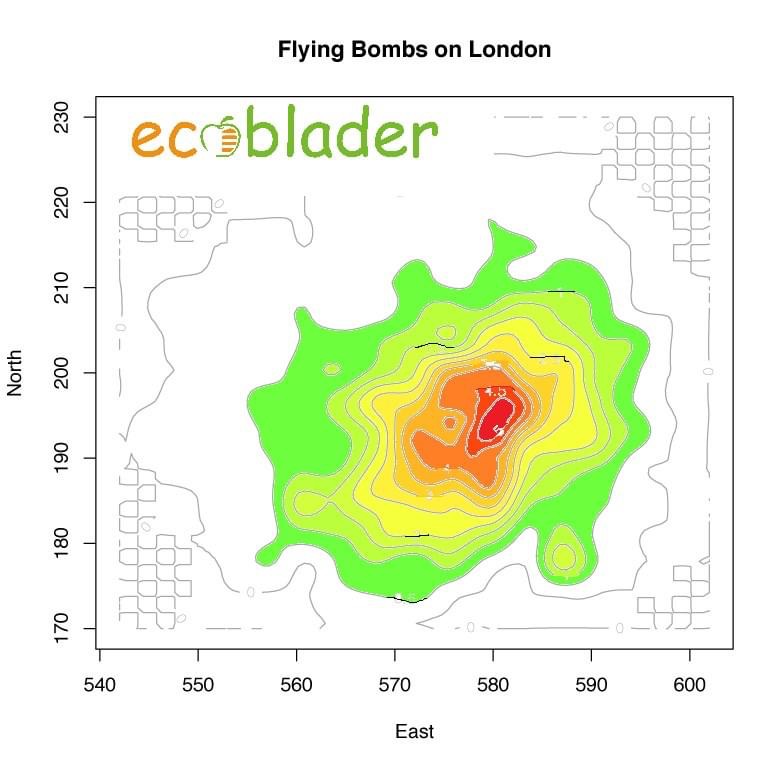
Như có thể thấy, ở một số khu vực tập trung rất nhiều bom, lên tận đến khoảng 5 quả (vùng màu đỏ), trong khi đó, nhiều khu vực khác nhận chưa đến 1 quả. Vậy có lẽ nào quân Đức đã xác định được một số mục tiêu, và tập trung đánh vào những mục tiêu này?
Một người kém toán thống kê sẽ nghĩ như vậy, nhưng mọi thứ không đơn giản như thế. Để xác định xem liệu bom rơi có hoàn toàn ngẫu nhiên hay không, Clarke so sánh tỉ lệ bom rơi thực tế với phân phối Poisson (bạn nào đã học xác suất thống kê sẽ biết phân phối này, nó dùng để xác suất n sự kiện xảy ra trong một khoảng thời gian bằng nhau xác định, ví dụ như xác suất cứ 5 phút thì có 1 khách hàng vào quán). Theo phân phối Poisson, thì nếu bom rơi là ngẫu nhiên, nó sẽ giống như sau (cột thứ hai):
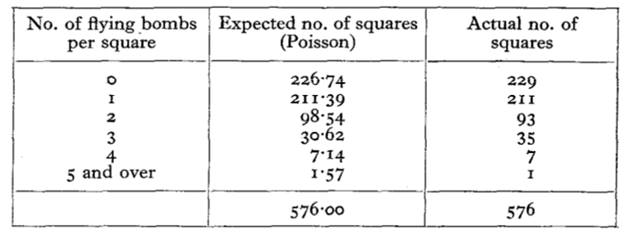
Như các bạn có thể thấy, phân phối bom rơi thực tế rất gần với phân phối Poisson ngẫu nhiên. Sau một số kiểm định thống kê đơn giản, Clarke khẳng định rằng bom rơi tự nhiên gần với phân phối Poisson, quân Đức chẳng biết gì cả, và cứ thả bom đại vậy thôi, không có thông tin mật bị rò rỉ, không có gì đáng lo ngại.
Phân phối Poisson được ứng dụng rất nhiều trong việc dự báo, ví dụ như tính toán số lượng quầy phục vụ khách chẳng hạn. Giả sử một siêu thị nọ có trung bình 5 khách ra quầy tính tiền mỗi 2 phút (và mỗi khách thường tính tiền xong trong khoảng 2 phút). Câu hỏi đặt ra lúc này là, liệu siêu thị nên lập bao nhiêu quầy tính tiền.
Người bình thường sẽ trả lời bằng cảm quan. Có người nghĩ rằng 5 là đủ, có người thì 10, có người thì 20 quầy cho chắc ăn. Vì mỗi quầy tăng thêm là thêm chi phí, còn nếu ít quầy khách đợi khách sẽ nổi quạu, nên ta phải tính toán thật chính xác để ra quyết định đúng. Theo công thức phân phối Poisson (bạn có thể Google xem), ta có bảng sau:
| Số khách/2 phút | Xác suất | Xác suất cộng dồn |
| 0 | 0.67% | 0.67% |
| 1 | 3.37% | 4.04% |
| 2 | 8.42% | 12.47% |
| 3 | 14.04% | 26.50% |
| 4 | 17.55% | 44.05% |
| 5 | 17.55% | 61.60% |
| 6 | 14.62% | 76.22% |
| 7 | 10.44% | 86.66% |
| 8 | 6.53% | 93.19% |
| 9 | 3.63% | 96.82% |
| 10 | 1.81% | 98.63% |
| 11 | 0.82% | 99.45% |
| 12 | 0.34% | 99.80% |
| 13 | 0.13% | 99.93% |
| 14 | 0.05% | 99.98% |
| 15 | 0.02% | 99.99% |
| 16 | 0.00% | 100.00% |
| 17 | 0.00% | 100.00% |
| 18 | 0.00% | 100.00% |
| 19 | 0.00% | 100.00% |
| 20 | 0.00% | 100.00% |
| 21 | 0.00% | 100.00% |
Như có thể thấy, với số quầy là 10, thì 98.63% khả năng là khách không phải chờ tới lượt. Một ngày làm việc 18 tiếng, tức là 540 lần 2 phút, vậy thì nếu có 10 quầy, thì chỉ có khoảng hơn 7 lần khách phải chờ tới lượt mình. Nếu tăng thêm một quầy lên 11 quầy, 99.45% khả năng khách không phải chờ, tức là khoảng 3 lần trong ngày là có trường hợp khách phải chờ tới lượt. Tăng 1 quầy, 1 nhân viên để giảm 4 lần có chuyện khách hàng phải chờ tới lượt trong siêu thị của mình mỗi ngày, bạn nghĩ có đáng hay không? Vậy bạn sẽ chọn bao nhiêu quầy?
Và nghĩ ngược lại, nếu cứ chia thời gian quan sát một siêu thị nào đó làm 2 phút, bạn sẽ đếm được mỗi đơn vị 2 phút có bao nhiêu lượt khách hàng, từ đó có thể suy ngược ra số khách trung bình của siêu thị trong mỗi khoảng thời gian được hay không?
Nếu áp dụng cách này, liệu bạn có thể đoán được số lượt khách trung bình của một fanpage, số lượt khách trung bình của một quán đang sang, hay thậm chí biết được những comment mua hàng trên fanpage “thầy” của bạn có thật sự là “tự nhiên” hay là sản phẩm của seeding hay không nhỉ?
Nếu biết phân phối Poisson, liệu bạn có thể tính được nên đặt bao nhiêu quầy tính tiền, nên có bao nhiêu bàn trong quán, hay nên thuê bao nhiều người trả lời fanpage không nhỉ?
Toán học cho bạn những công cụ để biết được những điều mà đối thủ của bạn đang cố giấu giếm. Cố mà học đi. Đừng bao giờ bỏ phí.